Residual Analysis
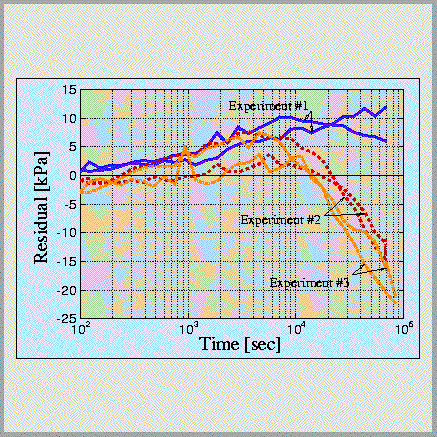 Assessing the goodness-of-fit is a crucial step in inverse modeling. If the goodness-of-fit criterion suggests that the model is an unlikely match to the data, then the estimated parameter set is bound to be meaningless. iTOUGH2 performs a detailed residual analysis which includes:
Assessing the goodness-of-fit is a crucial step in inverse modeling. If the goodness-of-fit criterion suggests that the model is an unlikely match to the data, then the estimated parameter set is bound to be meaningless. iTOUGH2 performs a detailed residual analysis which includes:
- Residual plot
- Statistics of residuals (mean, median, variance, absolute error, bias)
- Statistical model test
- Covariance matrix of calculated system response and residuals
- Normalized residuals
- Influence function
- Outlier identification
- Contribution of each data set and data type to the objective function
Estimation Error Analysis
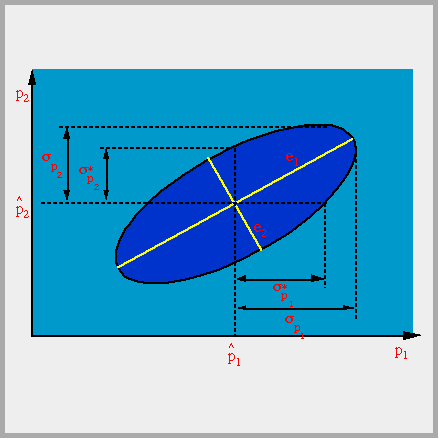 The covariance matrix of the estimated parameter set is calculated to assess estimation uncertainty. The error analysis in iTOUGH2 contains the following elements:
The covariance matrix of the estimated parameter set is calculated to assess estimation uncertainty. The error analysis in iTOUGH2 contains the following elements:
- Covariance matrix of estimated parameters
- Correlation matrix of estimated parameters
- Correlation chart
- Direct correlations between pairs of parameters
- Eigenanalysis of covariance matrix
- Measure of overall parameter sensitivity and parameter independence
- Correction procedure to account for non-linearities
Uncertainty Propagation Analysis
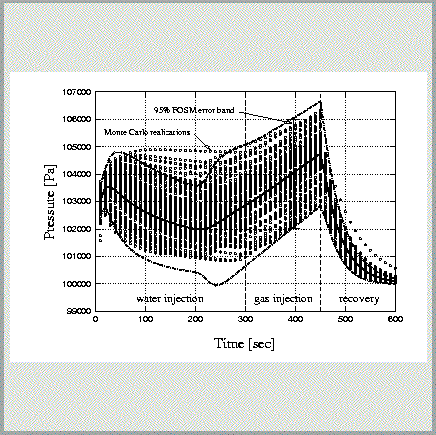 Uncertainty in the parameters entering a TOUGH2 model lead to uncertainties in the model predictions. Given the distributions of the parameters considered uncertain, iTOUGH2 calculates prediction uncertainty using one of the methods listed below. An application is described in James and Oldenburg [1997].
Uncertainty in the parameters entering a TOUGH2 model lead to uncertainties in the model predictions. Given the distributions of the parameters considered uncertain, iTOUGH2 calculates prediction uncertainty using one of the methods listed below. An application is described in James and Oldenburg [1997].
- Linear uncertainty propagation analysis
- Monte Carlo simulations; the predefined covariance matrix of correlated parameters is accurately reproduced using Empirical Orthogonal Functions.