Manual Page for Command >>> FISHER

---

Syntax
>>> FISHER

Parent Command
>> ERROR

Subcommand
-

Description
The estimated error variance s₀² represents the variance of the mean weighted residual and is thus a measure of goodness-of-fit:

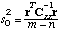The value s₀² is used in the subsequent error analysis. For example, the covariance matrix of the estimated parameters, C_pp, is directly proportional to the scalar s₀². Note that if the residuals are consistent with the distributional assumption about the measurement errors (i.e., matrix C_zz), then the estimated error variance assumes a value close to one. s₀² is also an estimate for the true or a priori error variance sigma₀². It can be shown that the ratio (s₀²/sigma₀²) follows an F-distribution with the two degrees of freedom f₁=m-n, and f₂=infinity. Therefore, it can be statistically tested to see whether the final match deviates significantly from the modeler’s expectations, expressed by matrix C_zz. This is called the Fisher Model Test. The user must decide whether the error analysis should be based on the a posteriori or a priori error variance (see commands >>> POSTERIORI and >>> PRIORI, respectively). The decision can also be delegated to the Fisher Model Test according to the following table:

Fisher Model Test	Error Variance	Comment
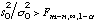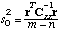		error either in the functional or stochastic model
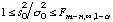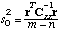		model test passed
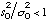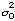		probably error in stochastic model

Example
> COMPUTATION
>> ERROR
>>> let the FISHER model test decide whether the
a priori or a posteriori error variance should be used
>>> confidence level 1-ALPHA : 95 %
<<<

 

See Also
>>> ALPHA | >>> POSTERIORI | >>> PRIORI

---