Manual Page for Command >>> MONTE CARLO

Syntax
>>> MONTE CARLO (SEED: iseed) (GENERATE) (CLASS: nclass)

Parent Command
>> ERROR

Subcommand
-

Description
This command performs Monte Carlo simulations to determine the uncertainty of model predictions as a result of parameter uncertainty. The general procedure is as follows:

(1) a probability distribution is defined for each uncertain parameter;
(2) parameter values are randomly sampled from their respective distributions;
(3) sampled parameter values are randomly combined to obtain a parameter vector;
(4) a TOUGH2 simulation is performed and the results at the specified observation points are stored;
(5) steps (3) through (4) are repeated;
(6) the ensemble of the modeling results can be statistically analyzed.

The type of distribution can be specified for each parameter in the respective parameter definition block (see command >>>> UNIFORM or >>>> NORMAL). The mean is given by the initial guess (see command >>>> GUESS), and the standard deviation by command >>>> DEVIATION (p). The generated parameter value is rejected if outside the specified range (see command >>>> RANGE). The number of Monte Carlo simulations, n_MC, must be provided in block >> CONVERGE using command >>> SIMULATION, i.e., by specifying the maximum number of TOUGH2 simulations. The number of Monte Carlo simulations n_MC can be considered sufficient if:

(1) the selected probability density function of the input parameters is reasonably well approximated by the histogram of the randomly generated parameter values. If correlations among the parameters are to be taken into account, use command >>> EMPIRICAL ORTHOGONAL FUNCTIONS. Keyword GENERATE can be used in combination with various seed numbers (keyword SEED) and values for n_MC (command >>> SIMULATION) to generate histograms of the input parameters without actually performing Monte Carlo simulations. Once a satisfactory distribution of the input parameters is achieved, the Monte Carlo simulations can be invoked by simply deleting keyword GENERATE.

(2) the histogram of the model predictions allows for a statistical analysis. That means that a sufficient number of realizations (= simulation results) should fall within each interval used to calculate probabilities. For example: The probability that TCE concentrations cTCE fall within the interval [a,b] is approximated by:

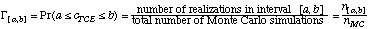Therefore, the minimum number of Monte Carlo simulations, nMC(min), should be large enough so that P remains constant, i.e. independent of nMC. This condition is fulfilled for relatively small values of nMC in the case of intervals around the mean, where n[a,b] is usually large due to the high probability density. However, if we are interested in the tail of the distribution, for example to calculate the (low) risk that TCE concentrations exceed a certain standard, then the number of Monte Carlo simulations required is much higher.

(3) The minimum number of Monte Carlo simulations must be increased if the number of uncertain parameter increases because more parameter combinations are possible.

(4) From experience, the number of Monte Carlo simulations can be as low as 50 and as high as 2000 or greater.

Histograms of the input parameters and output variables as printed to the iTOUGH2 output file. By default, the interval between the smallest and highest value is subdivided into sqrt(nMC) classes. The number of classes can be changed using keyword CLASS. The standard plot file contains all output sets from nMC simulations, where each set contains the model result as a function of time. A second plotfile is generated with “_mc” in the file name. In this second plot file, each curve represents the ensemble of the model output at one point in time. Denoting the number of output sets, for which prediction uncertainty is to be studied, by nSET, and the number of times by nTIMES, then the standard plot contains nSET*nMC curves, each curve consisting of nTIMES points. The second plotfile contains nSET*nTIMES curves, each consisting of nMC points.

Example
> PARAMETER >> ABSOLUTE permeability >>> MATERIAL : ROCK_ >>>> generate NORMAL distribution >>>> of LOGARITHM >>>> with mean (GUESS) : -16.0 >>>> standard DEVIATION : 1.0 >>>> in the RANGE : -18.5 -13.5 <<<< <<< >> POROSITY >>> MATERIAL : ROCK_ >>>> VALUE >>>> UNIFORM distribution >>>> RANGE : 0.02 0.10 <<<< <<< <<

> OBSERVATION
>> TIMES: 20 EQUALLY spaced in MINUTES
3.0 60.0

>> PRESSURE
>>> ELEMENT: PRE_0
>>>> NO DATA
>>>> WEIGHT: 1.0
<<<<
<<<
<<

> COMPUTATION
>> ERROR propagation analysis by means of
>>> : 1000 MONTE CARLO (SEED number is: 7777) using
>>> LATIN HYPERCUBE sampling
<<<
<<