Manual Page for Command >>> ANDREW

Syntax
>>> ANDREW: c

Parent Command
>> OPTION

Subcommand
-

Description
This command selects a robust estimator named Andrews. Given this estimator, the objective function to be minimized is the sum of the cosine functions g(y), where y is the weighted residual:

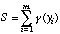where:

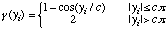with:

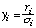This objective function does not correspond to a standard probability density function. It has the general characteristic that the weight given individual residuals first increases with deviation, then decreases to reduce the impact of outliers. The parameter c indicates the deviation at which residuals are considered to be outliers. If the measurement errors happen to be close to a normal distribution with standard deviation sigma, then the optimal value for the constant c is c=2.1. Note that this objective function can be minimized using the standard Levenberg-Marquardt algorithm which is designed for a quadratic objective function. Since (1-cosine) can be reasonably well approximated by a quadratic function for small y_i, the Levenberg-Marquardt algorithm is usually quite efficient.

Example
> COMPUTATION >> OPTION >>> use the robust estimator ANDREW with a constant c : 1.5 <<< <<