Syntax
>>> LEVENBERG-MARQUARDT (IDENTITY/EIGENVALUE) (SUPER/TRUNCATE (: (-)trunc))
Parent Command
>> OPTION
Subcommand
-
Description
This command selects the Levenberg-Marquardt algorithm to minimize the objective function. This is the default minimization algorithm. The Levenberg-Marquardt algorithm combines the robustness of a steepest descent method with the efficiency of a Gauss-Newton step (see command >>> GAUSS-NEWTON):
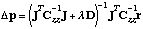where the Tikhonov matrix D is a diagonal matrix with elements
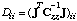Alternatively, the Tikhonov matrix can be the identity matrix (keyword IDENTITY), or a diagonal matrix with the inverse of the squared eigenvalues of the Fisher Information matrix, scaled by the maximum squared eigenvalue (keyword EIGENVALUE). The parameter space can be truncated (keyword TRUNCATE) based on the eigenvalues of the Fisher Information matrix. Parameter trunc defines the cut-off value as a fraction of the eigenvalue to the maximum eigenvalue (default: 10-6). If given as an integer, the top INT(trunc) parameters will be selected. If trunc is a negative integer, more parameters are added as iterations proceed, with all parameters included for the final iteration. If keyword SUPER is present, superparameters will be created (see Tonkin and Doherty [WRR, 41, W10412, doi:10.1029/2005WR003995, 2005]).
The Levenberg-Marquardt method switches continuously from a gradient method (large lambda, see command >>> LEVENBERG) far from the minimum to a Gauss-Newton step as the minimum is approached and lambda is reduced.
Example
> COMPUTATION
>> OPTION
>>> use LEVENBERG-MARQUARDT minimization algorithm (default)
<<<
>> CONVERGE
>>> initial LEVENBGERG parameter lambda is : 0.001 (default)
>>> MARQUARDT parameter nue is : 10.000 (default)
<<<
<<
See Also
>>> ANNEAL | >>> GAUSS-NEWTON | >>> GRID SEARCH | >>> LEVENBERG | >>> MARQUARDT